图形系统和模型
图形流水线
计算机图形学分为两个阶段:
从模型到屏幕空间的几何建模
在屏幕空间中创建所需的图像
图形流水线分为两个部分
Modeling Pipeline

3D Model Coordinates
- 您可以定义模型的各个部分,无论它们的坐标是什么
- 您使用建模转换将模型的各个部分放在一起,然后将模型放置在一个世界空间中
3D World Coordinates
- 场景的所有部分都被放在同一个3D坐标系统中
- 场景是独立于观察者的
3D Eye Coordinate System
- 当有一个观察者与一个观察者上下文,这个场景就成为图像
放置在世界空间的一个观察者(或摄像机)拥有一个位置与方向
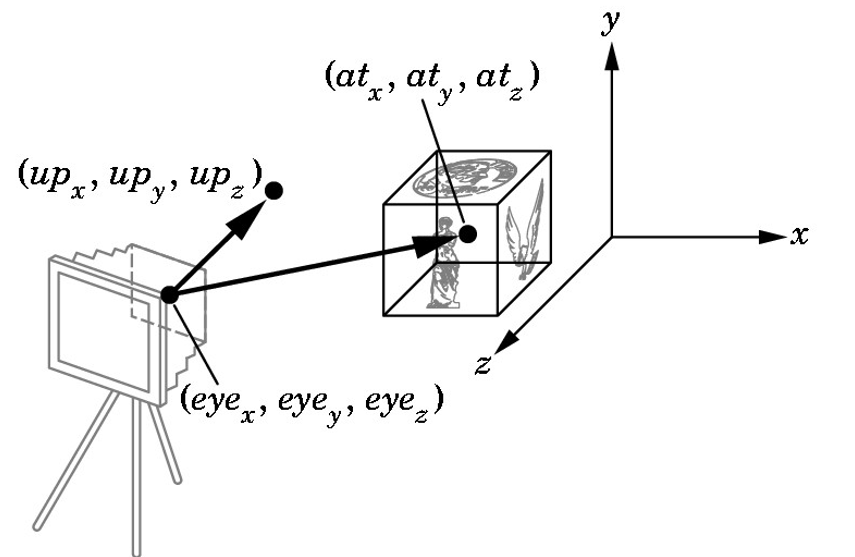
2D Eye Coordinates
透视投影与正交投影
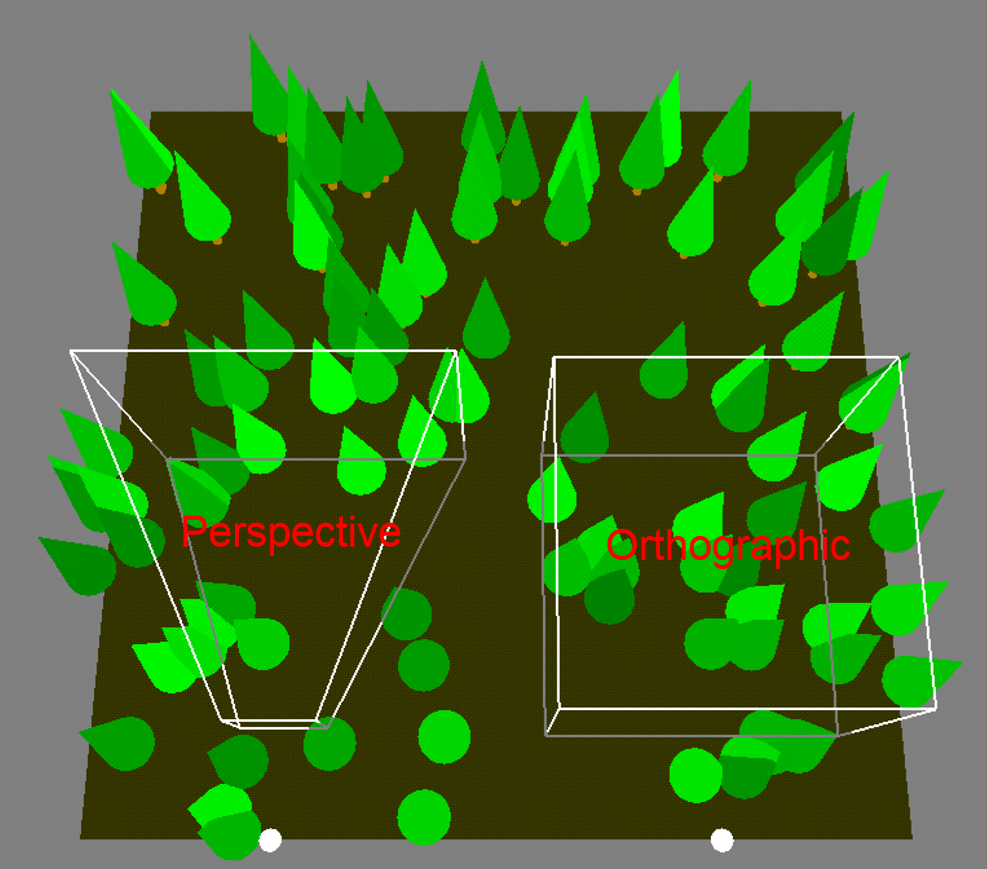
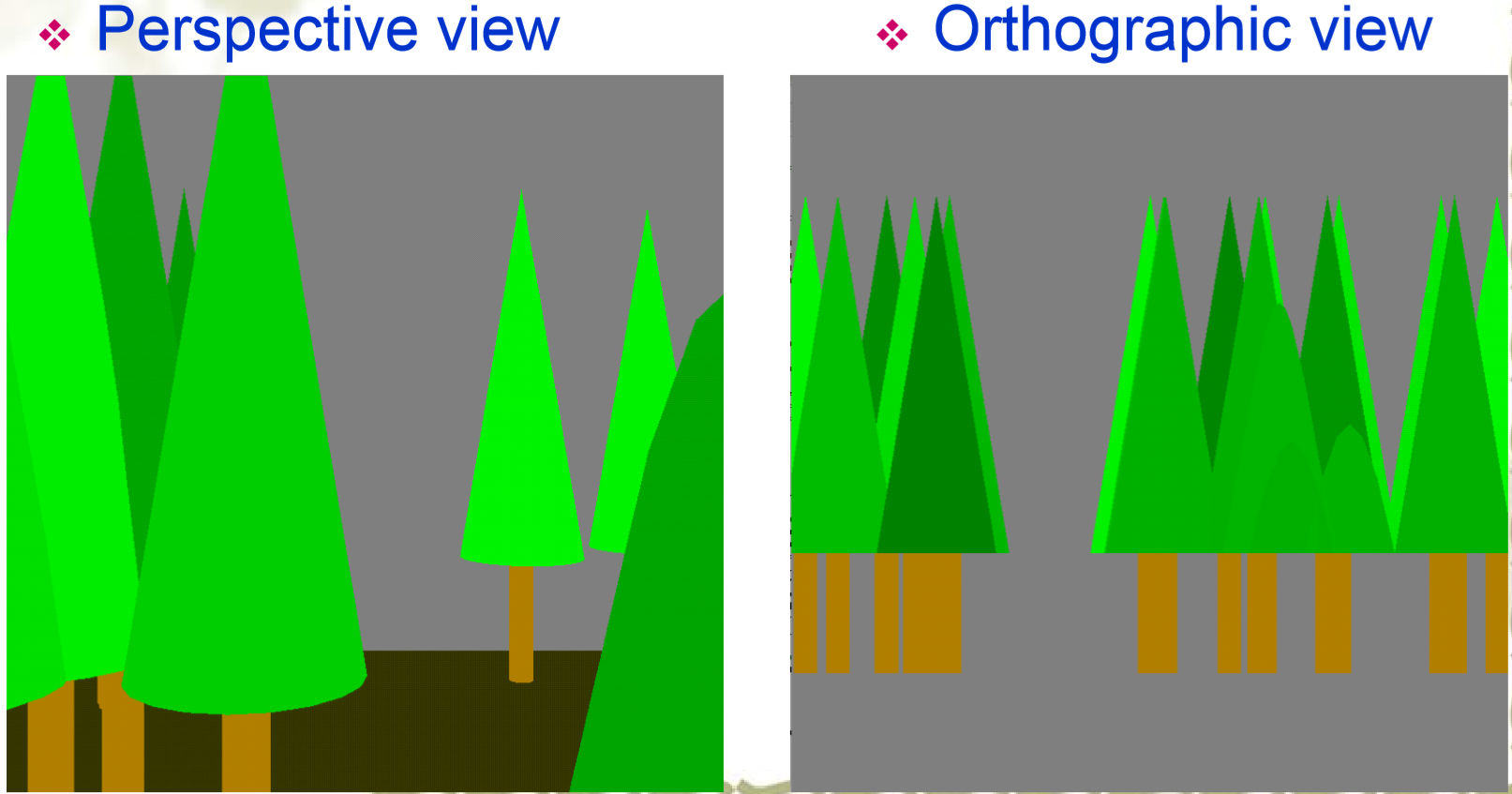
将每个点投影到平面上对应的点使得场景被转换到这个坐标系
在这个视图中深度信息会丢失
2D Screen Coordinates
2D eye coordinates 被放缩到屏幕维度
产生的实际坐标值被截断为屏幕上像素地址匹配的整数坐标
Rendering Pipeline
The modeling pipeline 只是在不同的空间映射顶点,所有顶点最终经过处理,在帧缓冲中形成一个图像
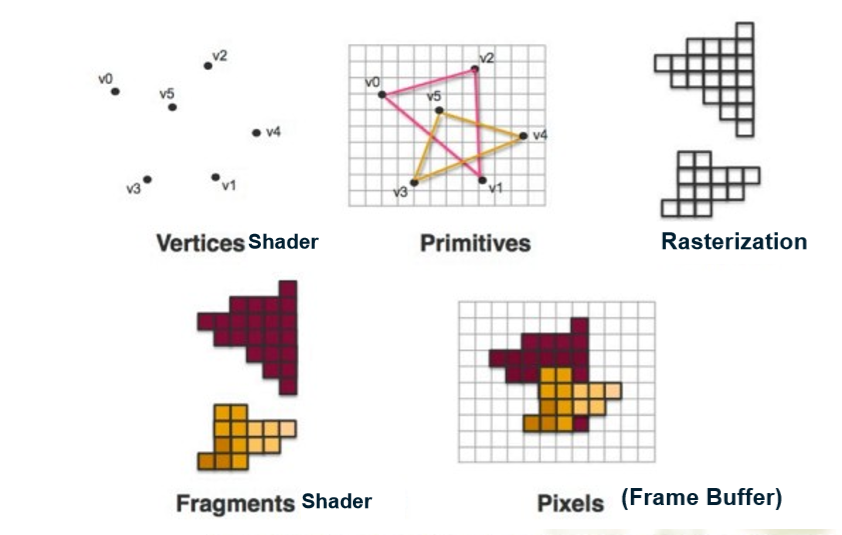
三色定理
人类视觉系统有两种传感器
- 杆状细胞(Rods):单色,夜视,感知亮度
- 锥状细胞(Cones):颜色敏感
人眼对红、绿、蓝最为敏感,人的眼睛像一个三色接收器的体系,大多数的颜色可以通过红、绿、蓝三色按照不同的比例合成产生。同样,绝大多数单色光也可以分解成红、绿、蓝三种色光,这是色度学的最基本的原理,也称三原色原理
屏幕是一个发射显示器,而不是反射
图形学编程
OpenGL 介绍
- OpenGL是一个状态机,它的函数有两种类型
- 图元生成
- 状态改变
GLSL(OpenGL Shading Language)
- GLSL是一种类C风格的着色器语言
OpenGL图元
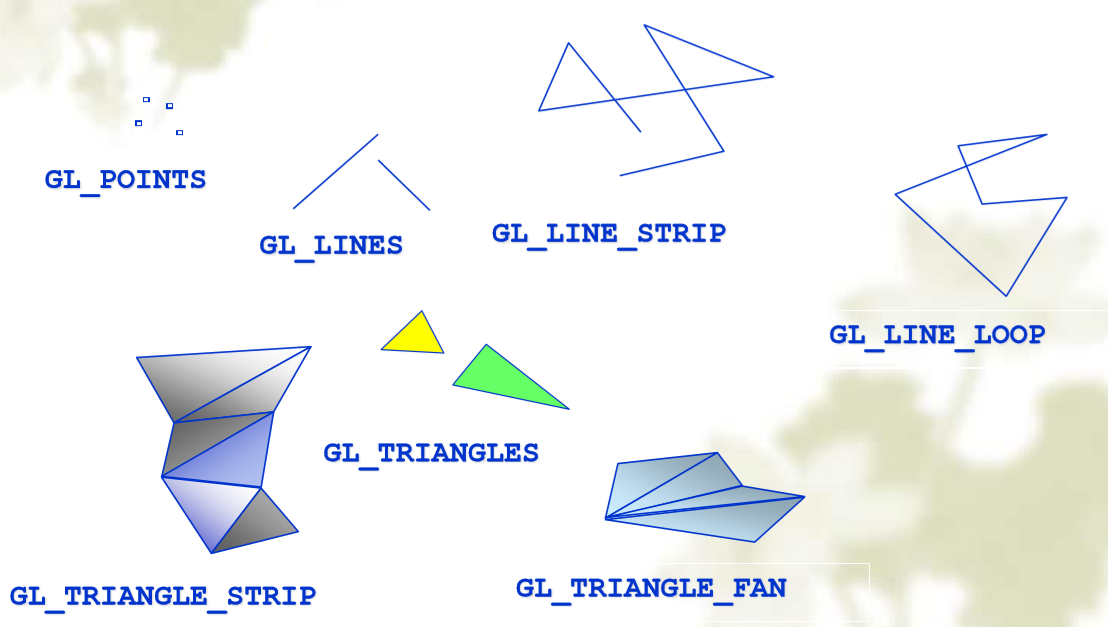
VAO(Vertex Array Object)
- 绑定了所有需要的顶点数据(位置,颜色。。。)
VBO(Vertex Buffer Object)
- 缓冲对象让我们可以一次性传输大量数据到GPU
几何对象和变换
反射向量
平面方程
碰撞检测算法
比较两个包围球或者包围盒:两个球心距离小于两个半径的和,则可能碰撞
可能碰撞时,一个物体的每个三角形与另一个包围体比较,假设是包围球:比较三角形的每个顶点,如果顶点与球心距离小于三角形最长边 + 球的半径,则可能碰撞;或者比较三角形外接圆与包围球,如果外接圆心与球心的距离小于外接圆半径 + 球的半径,则可能碰撞
比较两个三角形是否碰撞:一个三角形的每个顶点是否在另一个三角形平面的一边,即$Ax + By + Cz + D > 0$ 或 $Ax + By + Cz + D < 0$,如果在一边则不会碰撞,否则可能发生碰撞
判断一个三角形是否与另一个三角形相交:一个三角形的边$Q_0Q_1$与另一个三角形平面的交点Q是否在另一个三角形$P_0P_1P_2$里面,即以下三个不等式同时成立
则Q在三角形$P_0P_1P_2$里面
基本变换
齐次坐标
我们使用齐次坐标来将所有的转换表示为矩阵,并允许它们很容易地组合在一起:$P’ = (M3(M2 (M1 *P)))$
- 在齐次坐标,一个3D点可以表示为$ P = (x,y,z,1)^\top $
平移
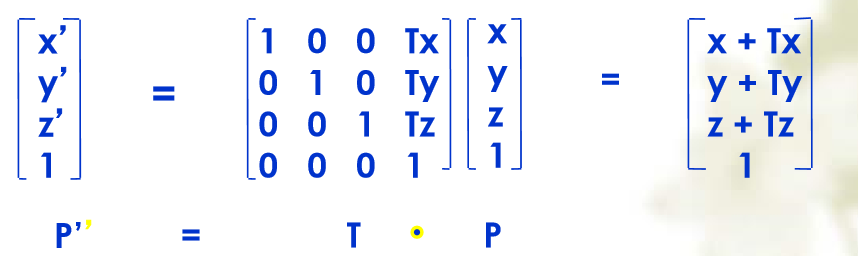
- 逆矩阵: $T^{-1}(d_x, d_y, d_z) = T(-d_x, -d_y, -d_z) $
缩放
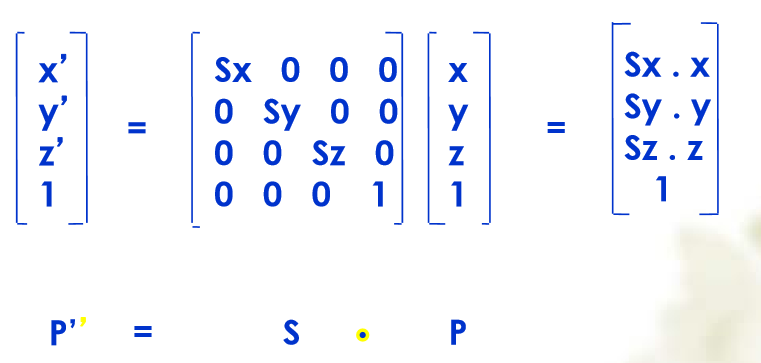
- 逆矩阵:$S^{-1}(s_x, s_y, s_z)= S(1/s_x, 1/s_y, 1/s_z)$
旋转
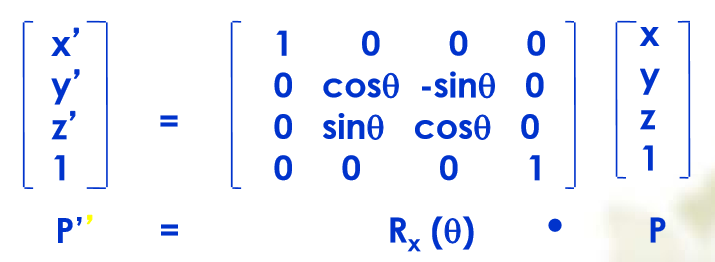
- 逆矩阵: $ R^{-1}(\theta) = R(-\theta) = R^\top(\theta) $
错切变换

投影和视见变换
投影矩阵
投影中心在原点
投影到 z = d 的平面的投影矩阵
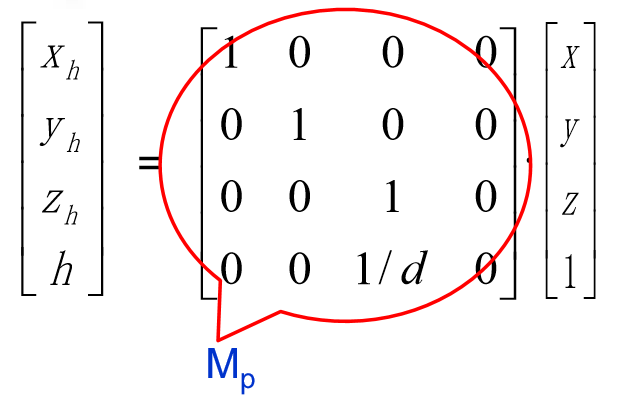
投影中心不在原点
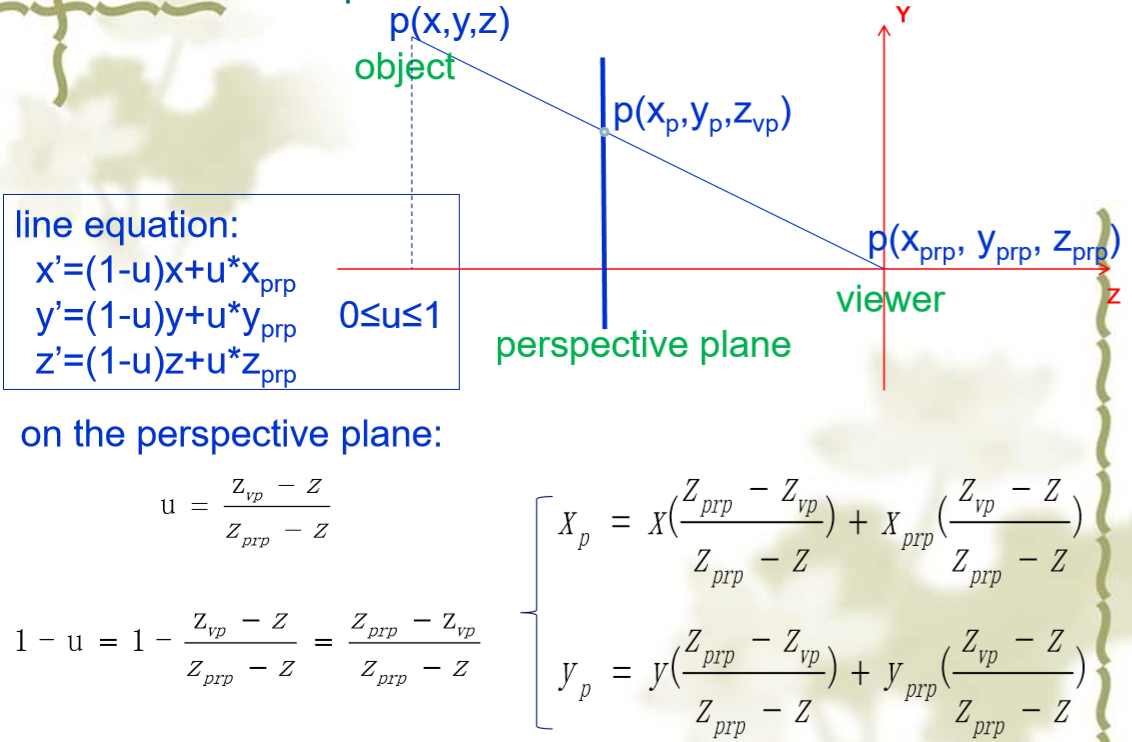
投影规范化
使用平移和旋转变换将照相机坐标系下的顶点变换到默认的视见体的内部
平行投影
通过平移把指定视见体的中心移到规范视见体的中心(原点)
通过缩放指定的视见体使得它的每条边的长度为2
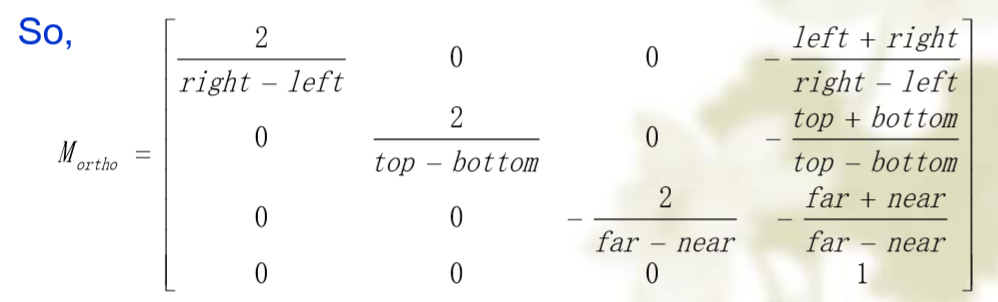
透视投影

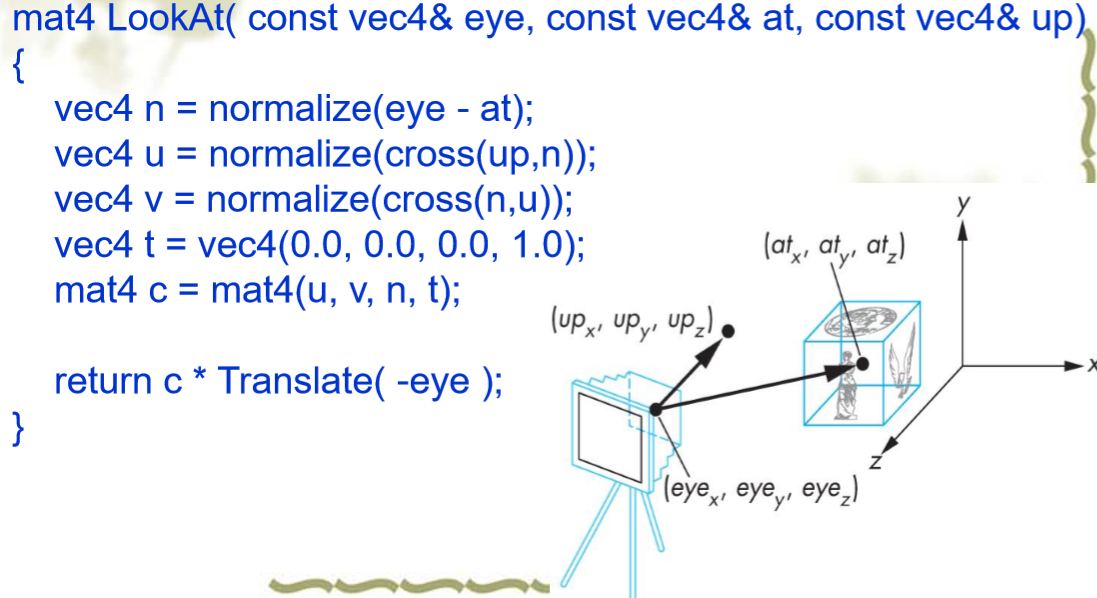
视见变换
指定眼睛(或者视图参考点)作为原点
将视图平面法向量n指定为z轴
将视图向量(VUP) v指定为y轴
x轴(第三个向量u)可以用叉乘计算:u = v×n
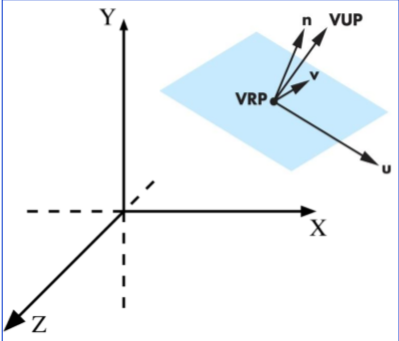
将世界坐标系转换为眼睛坐标系
视口
视口是窗口的一个你可以在上面绘画的矩形区域
默认的视口是整个窗口
可以定义一个更小的窗口使得所有绘制被限制在那个区域
你可以为每个视口端口使用单独的建模
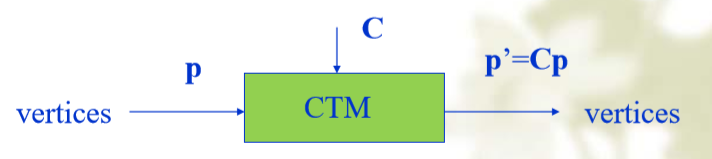
CTM(Current Transformation Matrix)
从概念上讲,有一个4×4的齐次坐标矩阵,即当前变换矩阵(CTM),它是状态的一部分,适用于沿管道向下传递的所有顶点
光照和着色
光照概念
光线从光源照射到物体上,透射出反射光、透明光和吸收光(不可见)。
反射光包括漫射光和反射光,反射光与物体的材质有关
光照模型
我们使用的是局部光照模型(Local Illumination Model):光线只来自定义在场景中的光源,忽视被其他物体或者表面反射的光
光照被看作由三个部分组成
环境光(Ambient)
- 不关心光照位置
- 不关心观察者位置
不关心表面法向量
漫反射光(Diffuse)
区域对光来说是否可见取决于光的角度——光向量与平面法向量的点乘
镜面反射光(Specular)
取决于反射光与观察方向的角度
K:感光度,改变光的衰减速率

没有物理基础,但在实践中是可行的
另一种光照模型是Blinn-Phong光照模型,唯一不同的地方是计算镜面反射光是使用法向量点乘观察方向与入射方向的半角
所有光使用RGB颜色模型
表面定向与材质
- 为了使用光照,你必须获得每个顶点的法向量与每个对象的材质
法向量
- 可以计算为两个相邻边的外积
光的属性
光的类型
- 点光源
- 定向光
- 聚光
- 环境光
光的位置
- 光的方向
- 聚光灯的方向和截止
- 光的衰减
- 光的颜色
光照着色
- 计算图形对象各部分的颜色,尤指多边形
Constant(Flat) Shading
对于多边形只计算其上的一个点,生成的结果被分配给多边形覆盖的所有像素
效率很高但通常十分粗糙
着色的离散变化(马赫带,Mach band)通常发生在constant shading
Gouraud (Smooth) Shading
平面的每一个顶点都进行渲染计算
每个顶点都会有一个法向量,或者是由相邻的几个平面求平均得到的法向量
平面的其他像素颜色通过对颜色线性插值获取
Phong Shading
对法向量进行线性插值
对每个像素使用局部光照模型
全局光照
不止考虑来自场景中的光,也考虑反射光
更复杂,但更真实
热辐射、射线追踪
渲染——从顶点到片段
线段裁剪算法
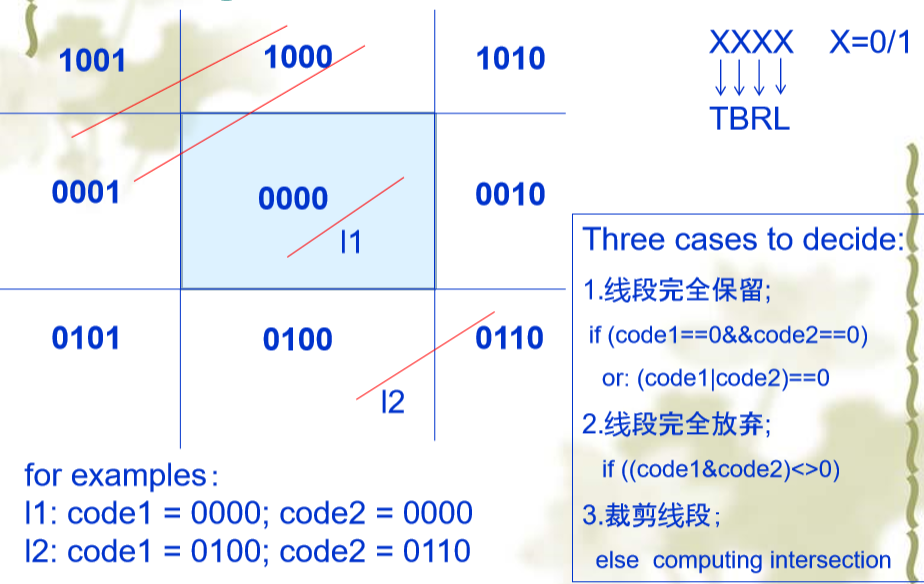
Cohen-Sutherland 线段裁剪算法
该算法有4种情况
线段的两点都在区域内
线段的两点都在区域外并且在一条边界的同一侧
一个点在区域内一个点在区域外
两点都在区域外但不在一条边界的同一侧
可以将情况的两点进行编码,然后两点运算来裁剪线段
梁友栋-Barsky 线段裁剪算法
使用参数方程求出与裁剪窗口四条边的交点,通过交点顺序来判断是否需要裁剪
多边形填充区域裁剪
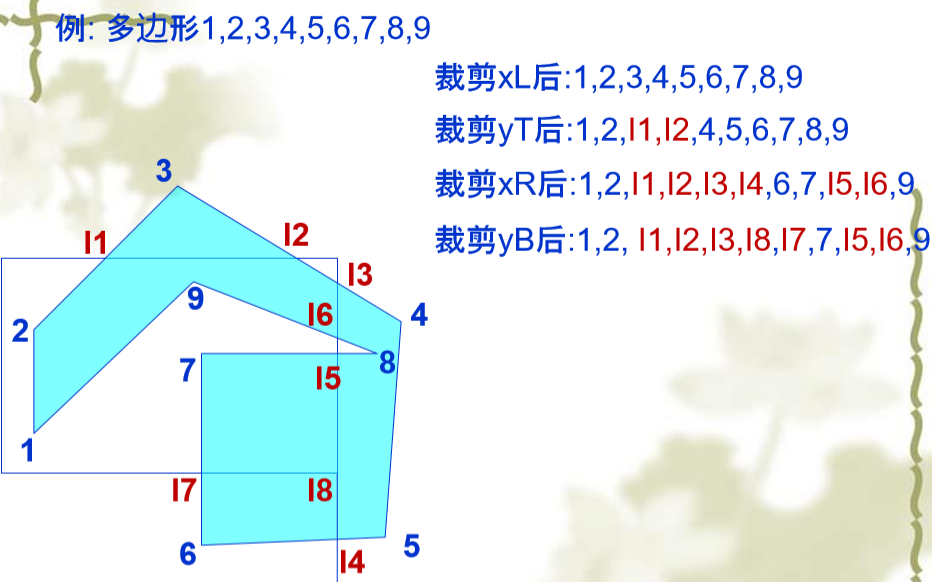
光栅化
根据一组顶点确定需要着色的像素
生成一组片段
片段有一个位置(像素位置)和其他属性,比如颜色和纹理坐标,这些属性是通过在顶点上插入值来确定的
DDA 算法
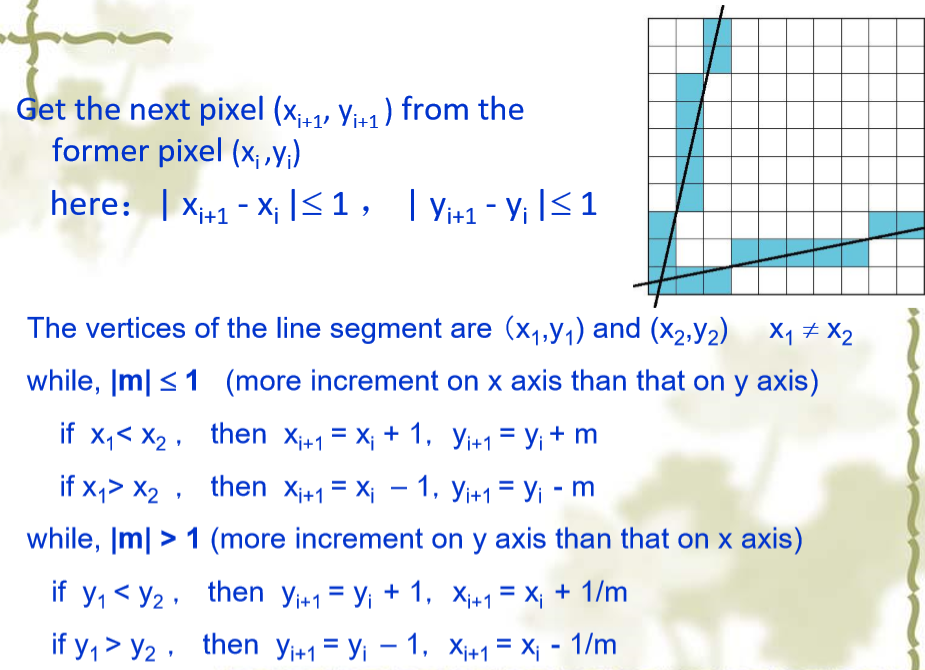
行扫描转换——Bresenham Algorithm
- 判断交点更接近$yi$还是$y{i+1}$

扫描转换多边形——扫描线填充算法
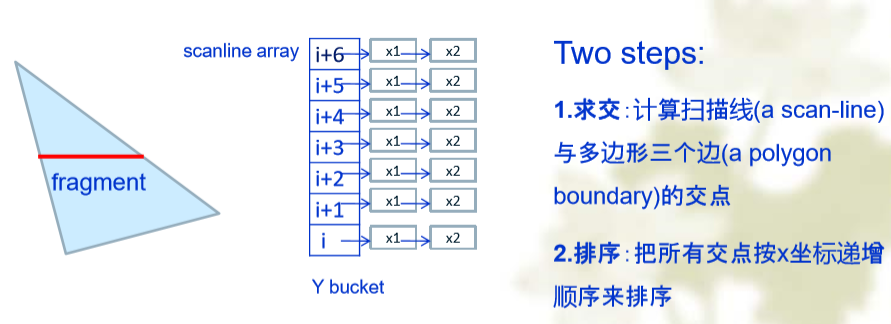
隐藏面消除
z-Buffer 算法
- 深度缓冲区与帧缓冲区相同
- 保存最近的交点的距离
画家算法
- 从后往前渲染
- 对所有多边形进行深度排序
- 如果有多个多边形循环重叠,需要把多边形分为多个部分
反走样
- 计算线与附近像素方块的重叠比例,像素颜色计算公式
多边形混叠
- 像素的颜色取决于多多边形的颜色
离散技术
写缓存模式
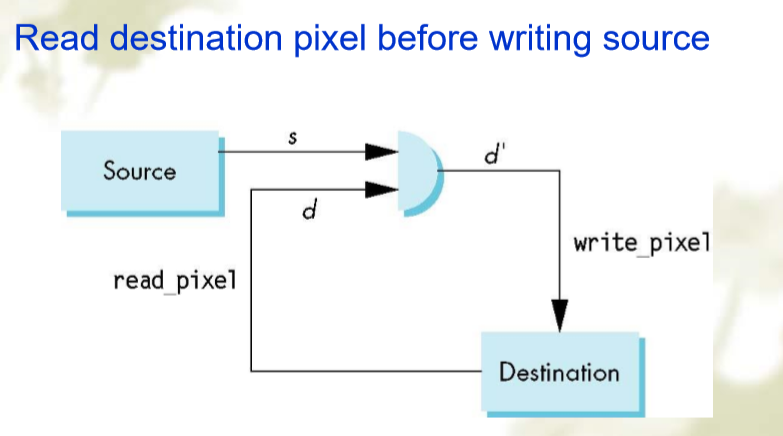
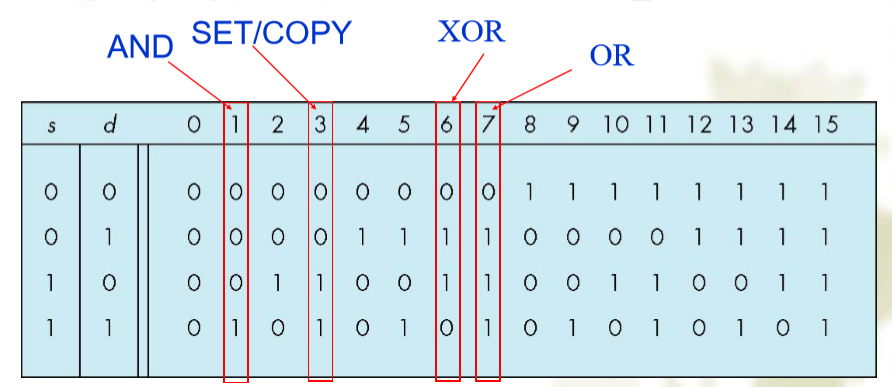
- 重点注意XOR写入模式,即模式6,有如下特性
纹理贴图
凹凸贴图
在Gouraud shading中,光强度是在顶点处计算的。线上其他像素的强度由两个顶点的强度混合而成
在凹凸贴图中,光强度是在每个像素处计算的。使用原始曲面的法线。(注意曲线仍然是用直线近似。)
层级建模方法
全局光照
射线追踪
对于每个射线,寻找最近的阻挡光路的物体
计算这个物体的像素颜色
可以确定物体的阴影,光线是否会到达那个表面
详情借鉴别人的博客
辐射度算法
- 辐射度算法的原理就是模拟真实世界中的光照原理,在场景中的每个位置收集所有在该位置所能看到的光照信息,然后对这些颜色信息进行汇总处理,作为最终该位置的颜色并对当前的位置进行着色。在现实世界中,这个位置就代表了无穷多个无限小的像素点,但在计算机中却不可能做到这样一点,因此只能进行近似的模拟操作,这就是将几何空间场景进行分割处理,得到一些相对于整个场景来说很小的多边形面片,然后以这些面片为单位来代替现实世界中的无限小的像素点进行渲染着色。当然,如果我们对整个场景分割得越发细小,得到的最终光照效果也就是越好,但随之而来的代价就是渲染的时间越长。讲的不错的一篇博客
最后附上找到的一个学习OpenGL编程的很好的教程

